연구실 스터디를 위해 Simon J.D. Prince의 Understanding Deep Learning의 13챕터 GNN에 대해서 공부하며 정리한 글입니다.
그래프를 다루는데 존재하는 3가지 문제점
- 첫째, 토폴로지가 가변적이기 때문에 충분히 표현력이 풍부하고 이러한 변화에 대응할 수 있는 네트워크를 설계하기가 어렵다.
- 둘째, 그래프의 크기가 방대할 수 있다. 예를 들어 소셜 네트워크 사용자 간의 연결을 나타내는 그래프에는 10억 개의 노드가 포함될 수 있다.
- 셋째, 단일 모놀리식 그래프만 존재할 수 있으므로 많은 데이터 예제로 훈련하고 새로운 데이터로 테스트하는 일반적인 프로토콜이 항상 적절한 것은 아니다.
1. What is a graph?
1.1. Types of graphs
Heterogeneous graph: 다양한 유형의 노드와 엣지를 포함하는 그래프
Homogeneous graph: 모든 노드와 엣지가 같은 유형인 그래프
2. Graph representation
노드의 정보는 노드 임베딩 벡터에 저장되고, 엣지의 정보는 엣지 임베딩 벡터에 저장된다.
2.1. Properties of the adjacency matrix

- 인접 행렬 $\mathbf{A}^k$의 $(m, n)$은 노드 $m$에서 출발해 노드 $n$에 도달하는 경로 중 길이가 $k$인 것의 개수를 의미한다. (이때, 같은 노드를 재방문하는 것을 허용함)
- 여섯 번째 노드를 나타내는 원핫 벡터 $\mathbf{x}$와 인접 행렬을 곱하는 경우, 여섯 번째 노드에서 다른 노드까지 경로 중 길이가 $k$인 것의 개수를 나타낸다.
2.2. Permutation of node indices

- 그래프에서 노드 인덱스는 임의로 부여될 수 있다. 노드 인덱스를 재배열하면 노드 데이터 행렬 $\mathbf{X}$의 열이 재배열되고, 인접 행렬 $\mathbf{A}$의 행과 열이 재배열된다. 그러나, 그래프의 기본 구조는 변하지 않는다.
- 그런데 이는 그래프와 이미지 및 텍스트와는 다르다. 이미지에서 픽셀을 재배열하면 다른 이미지가 되고, 텍스트에서 단어를 재배열하면 다른 문장이 된다.
- 노드 인덱스를 교환하기 위해 순열 행렬(각 행과 각 열에 정확히 하나의 값이 1이고 나머지 값은 0인 행렬)을 곱한다. 앞에 곱하면 행이 재배열되고, 뒤에 곱하면 열이 재배열된다.
- 그래프에 적용되는 모든 처리는 이러한 순열에 무관해야 한다. 그렇지 않으면, 결과가 노드 인덱스의 선택에 따라 달라질 수 있다.
3. Tasks of graph neural networks
그래프 신경망은 노드 임베딩 $\mathbf{X}$와 인접 행렬 $\mathbf{A}$를 입력으로 받아 일련의 $K$ 계층을 통과하는 모델이다. 노드 임베딩은 최종적으로 산출 임베딩 $\mathbf{H}_K$를 계산하기 전에 각 레이어에서 업데이트되어 '숨겨진' 표현 $\mathbf{H}_k$를 생성한다.
이 네트워크의 시작 부분에서 입력 노드 임베딩 $X$의 각 열에는 노드 자체에 대한 정보만 포함된다. 마지막에 모델 산출물 $\mathbf{H}_K$의 각 열에는 그래프 내에서 노드와 그 컨텍스트에 대한 정보가 포함된다. 이는 트랜스포머 네트워크를 통과하는 단어 임베딩과 유사하다. 이는 처음에는 단어를 나타내지만 마지막에는 문장의 문맥에서 단어의 의미를 나타낸다.
3.1. Tasks of graph neural networks
- Graph-level tasks: 아래의 식과 같이 GNN의 최종 아웃풋 $\mathbf{H}_K$를 바탕으로 그래프에 대하여 클래스를 할당하거나 회귀값을 구할 수 있다. 여기서 스칼라 $\beta_K$와 $1 \times D$ 차원의 벡터 $\boldsymbol{\omega}_K$는 학습된 파라미터이다. 산출된 임베딩 행렬 $\mathbf{H}_K$에 1로 이루어진 열 벡터 $\mathbf{1}$을 곱하여 모든 임베딩을 합산한 후, 노드 수 $N$으로 나누어 평균을 계산한다.
$$Pr(y=1|\mathbf{X}, \mathbf{A})=\sigma[\beta_K + \omega_K \mathbf{H}_K \mathbf{1}/N]$$ - Node-level tasks: GNN의 최종 노드 임베딩 $\mathbf{h}_{K}^{(n)}$을 바탕으로 각 노드에 대하여 클래스를 할당하거나 회귀값을 구할 수 있다.
$$ Pr(y^{(n)}=1|\mathbf{X}, \mathbf{A})=\sigma[\beta_K + \omega_K \mathbf{h}_{K}^{(n)} ] $$ - Edge prediction tasks: GNN의 엣지에 대하여 두 노드의 관계성을 수치화할 수 있다.
$$ Pr(y^{(nm)}=1|\mathbf{X}, \mathbf{A})=\sigma[\mathbf{h}^{(m)T}\mathbf{h}^{(n)} ] $$
4. Graph convolutional networks
여기서는 공간 기반 컨볼루션 그래프 신경망, 줄여서 GCN에 초점을 맞춘다. 이러한 모델은 주변 노드의 정보를 aggregator로 취합하여 각 노드를 업데이트한다는 점에서 컨볼루션 방식이다. 따라서 relational inductive bias (즉, 이웃 노드의 정보를 우선시하는 편향)을 유도한다. 원본 그래프 구조를 사용하기 때문에 공간 기반이다.
GCN의 각 계층은 노드 임베딩과 인접 행렬을 입력받아 새로운 노드 임베딩을 산출하는 매개변수 $\Phi$를 가진 함수 $\mathbf{F}$이다. 따라서 네트워크는 다음과 같이 작성할 수 있다:
$$ \begin{align*} \mathbf{H}_1 \; & = \; \mathbf{F}[\mathbf{X}, \mathbf{A}, \phi_0] \\ \mathbf{H}_2 \; & = \; \mathbf{F}[\mathbf{H}_1, \mathbf{A}, \phi_1] \\ \mathbf{H}_3 \; & = \; \mathbf{F}[\mathbf{H}_2, \mathbf{A}, \phi_2] \\ \vdots \; & =\; \vdots \\ \mathbf{H}_{K} \; & = \; \mathbf{F}[\mathbf{H}_{K-1}, \mathbf{A}, \phi_{K-1}] \end{align*} $$
4.1. Equivariance and invariance
앞서 그래프에서 노드의 인덱싱은 임의적이고, 따라서 어떠한 노드 인덱스의 변경에도 그래프가 변경되지 않는다는 점을 언급하였다. 따라서 모든 모델은 이 속성을 존중해야 한다. 즉, 노드 인덱스의 재배열에 대해 각 계층은 동일한 출력을 보장해야 한다. 즉, 노드 인덱스를 재배열하면 각 단계의 노드 임베딩도 같은 방식으로 재배된다. 수학적으로 $\mathbf{P}$가 순열 행렬이라면, 우리는 다음과 같은 행렬을 가져야 한다:
$$ \mathbf{H}_{k+1} = \mathbf{F}[\mathbf{H}_{k}\mathbf{P}, \mathbf{P}^{T}\mathbf{A}\mathbf{P}, \phi_{k}] $$
Node classification 및 edge prediction 작업의 경우에도, 노드 인덱스의 재배열에 대해서 산출물이 동일해야 한다. 반면 그래프 수준 작업의 경우, 최종 계층은 그래프 전체의 정보를 집계하므로 노드 순서에 따른 산출물이 동일하다:
$$ y=\sigma[\beta_K + \omega_K \mathbf{H}_K \mathbf{1}/N]=\sigma[\beta_K + \omega_K \mathbf{H}_K \mathbf{P} \mathbf{1}/N] $$
이는 세그멘테이션과 이미지 classification이 기하학적 변형에 대해 독립적이어야 하는 경우와 유사하다. 컨볼루션 및 풀링 레이어는 평행이동과 관련하여 부분적으로 이를 달성하지만, 보다 일반적인 변환에 대해서도 이러한 특성을 정확히 보장하는지는 밝혀지지 않았다. 그러나 그래프의 경우 재배열에 대한 동등성 또는 불변성을 보장하는 네트워크를 정의할 수 있다.
4.2. Parameter Sharing
- 이미지 처리
- 완전 연결 신경망의 비효율성: 이미지의 모든 위치에서 객체를 별도로 인식해야 하므로 많은 매개변수가 필요
- 합성곱 층의 사용: 모든 위치를 동일하게 처리하여 매개변수를 줄이고, 모델이 이미지의 모든 부분을 동일하게 처리하도록 하는 귀납적 편향(inductive bias) 도입
- 그래프 처리
- 각 노드에 개별 매개변수 할당의 비효율성: 그래프의 각 위치에서 연결의 의미를 독립적으로 학습해야 하므로 많은 데이터와 매개변수가 필요
- 동일한 매개변수 사용: 모든 노드에서 동일한 매개변수를 사용하여 매개변수를 줄이고, 학습된 내용을 전체 그래프에 공유
- 합성곱의 원리와 그래프 적용
- 이미지 합성곱: 이웃 픽셀로부터 정보를 가중합하여 변수 업데이트 → 이웃은 고정된 크기의 사각형 영역으로 공간적 관계가 일정
- 그래프 합성곱: 각 노드가 서로 다른 수의 이웃을 가지며, 일관된 공간적 관계가 없으므로 공간적 의미가 존재하지 않는 매개변수를 사용해 정보를 공유
요약
이미지와 그래프 모두에서 효율성을 높이기 위해 동일한 매개변수를 사용하는 모델이 필요하다. 이미지는 합성곱 층을 통해, 그래프는 모든 노드에서 동일한 매개변수를 사용하여 처리 효율을 높인다. 그래프에서는 위치에 따른 일관된 관계가 없어 모든 노드에서 학습된 내용을 공유하는 모델이 필수적이다.
4.3. Example GCN layer
GCN 레이어는 그래프 구조를 활용하여 각 노드에서 이웃 노드의 정보를 집계하고 이를 바탕으로 노드 임베딩을 업데이트한다.
- 이웃 노드의 집계
각 노드 $n$의 $k$번째 레이어에서 이웃 노드들의 임베딩 $h$를 합산하여 집계한다.
$$ \textrm{agg}[n, k] = \sum_{m \in \text{ne}[n]} h^{(m)}_k $$
여기서 $\textrm{ne}[n]$은 노드 $n$의 이웃 노드들의 집합이다. - 선형 변환 및 비선형 활성화 함수 적용
현재 노드의 임베딩 $\mathbf{h}_k^{(n)}$와 집계된 값에 선형 변환 $\boldsymbol{\Omega}_k$를 적용하고, 편향 $\boldsymbol{\beta}_k$를 더한 후 비선형 활성화 함수 $\mathbf{a}$를 적용하여 업데이트한다.
$$ \mathbf{h}^{(n)}_{k+1} = \mathbf{a}\left[\boldsymbol{\beta}_k + \boldsymbol{\Omega}_k \cdot \mathbf{h}^{(n)}_k + \boldsymbol{\Omega}_k \cdot \textrm{agg}[n, k]\right] $$ - 행렬 연산을 통한 간결한 표현
행렬 연산을 사용하여 더 간결하게 표현할 수 있다. 노드 임베딩을 $D \times N$ 행렬 $\mathbf{H}_k$로 모으고, 인접 행렬 $\mathbf{A}$를 사용하여 이웃 노드들의 정보를 집계한다.
$$ \mathbf{H}^{(n)}_{k+1} = \mathbf{a}\left[\boldsymbol{\beta}_k \mathbf{1}^T + \boldsymbol{\Omega}k \mathbf{H}_{k} (\mathbf{A} + \mathbf{I})\right] $$
요약
이 GCN 레이어는 노드 인덱스의 순열에 대해 동일하게 작동하며, 어떤 수의 이웃 노드도 처리할 수 있고, 그래프 구조를 활용하여 관계 귀납적 편향 제공한다. 이는 전체 그래프에서 매개변수를 공유하여 효율적으로 학습할 수 있도록 한다.
5. Example: graph classification
신경망의 입력은 인접 행렬 $\mathbf{A} \in \mathbb{R}^{N \times N}$과 노드 임베딩 행렬 $\mathbf{X} \in \mathbb{R}^{C \times N}$이라고 하자. 이때 $N$은 그래프에 포함된 노드의 개수이고, $C$는 노드 임베딩 벡터의 차원이다. 임의의 차원 $D$를 갖는 가중치 행렬 $\boldsymbol{\Omega}_0 \in \mathbb{R}^{D \times C}$에 대하여 그래프 분류의 문제는 다음과 같이 나타낼 수 있다.
$$ \begin{align*} \mathbf{H}_1 \; & = \; \mathbf{a}\left[\boldsymbol{\beta}_0 \mathbf{1}^T + \boldsymbol{\Omega}_0 \mathbf{X} (\mathbf{A} + \mathbf{I})\right] \\ \mathbf{H}2 \; & = \; \mathbf{a}\left[\boldsymbol{\beta}_1 \mathbf{1}^T + \boldsymbol{\Omega}_1 \mathbf{H}_{1} (\mathbf{A} + \mathbf{I})\right] \\ \vdots \; & = \; \vdots \\ \mathbf{H}K \; & = \; \mathbf{a}\left[\boldsymbol{\beta}_{K-1} \mathbf{1}^T + \boldsymbol{\Omega}_{K-1} \mathbf{H}_{K-1} (\mathbf{A} + \mathbf{I})\right] \\ \textrm{f}\left[\mathbf{X},\mathbf{A}, \boldsymbol{\Phi} \right] \; & = \; \sigma \left[ \beta_K + \boldsymbol{\omega}_K \mathbf{H}_K \mathbf{1}/N\right] \end{align*} $$
이때 $\textrm{f}\left[\mathbf{X},\mathbf{A}, \boldsymbol{\Phi} \right]$는 확률을 나타내는 하나의 값이다.
5.1. Training with batches
- 그래프 병합
- 주어진 $I$개의 훈련 그래프 $\{\mathbf{X}_i, \mathbf{A}_i\}$가 있을 때, 각 그래프 $\mathbf{X}_i$와 인접 행렬 $\mathbf{A}_i$는 서로 다른 크기를 가질 수 있기 때문에 배치로 묶는데 어려움이 있다.
- 이 그래프들을 하나의 큰 그래프로 결합하여 병렬 처리할 수 있다. 이 때, 각 그래프는 서로 연결되지 않은 독립적인 구성 요소로 취급된다.
- 큰 행렬 생성:
- 모든 그래프의 노드 임베딩 행렬 $\mathbf{X}_i$를 하나의 큰 행렬 $\mathbf{X}$로 결합하고, 모든 그래프의 인접 행렬 $\mathbf{A}_i$를 하나의 큰 인접 행렬 $\mathbf{A}$로 결합한다.
- 예를 들어, $\mathbf{X}$는 모든 $\mathbf{X}_i$를 세로로 쌓아 올린 형태이고, $\mathbf{A}$는 모든 $\mathbf{A}_i$를 블록 대각선 형태로 배치하여 생성된다.
- 결과 처리: 각 그래프의 출력을 개별적으로 추출하여 처리한다.
6. Inductive vs. Transductive models
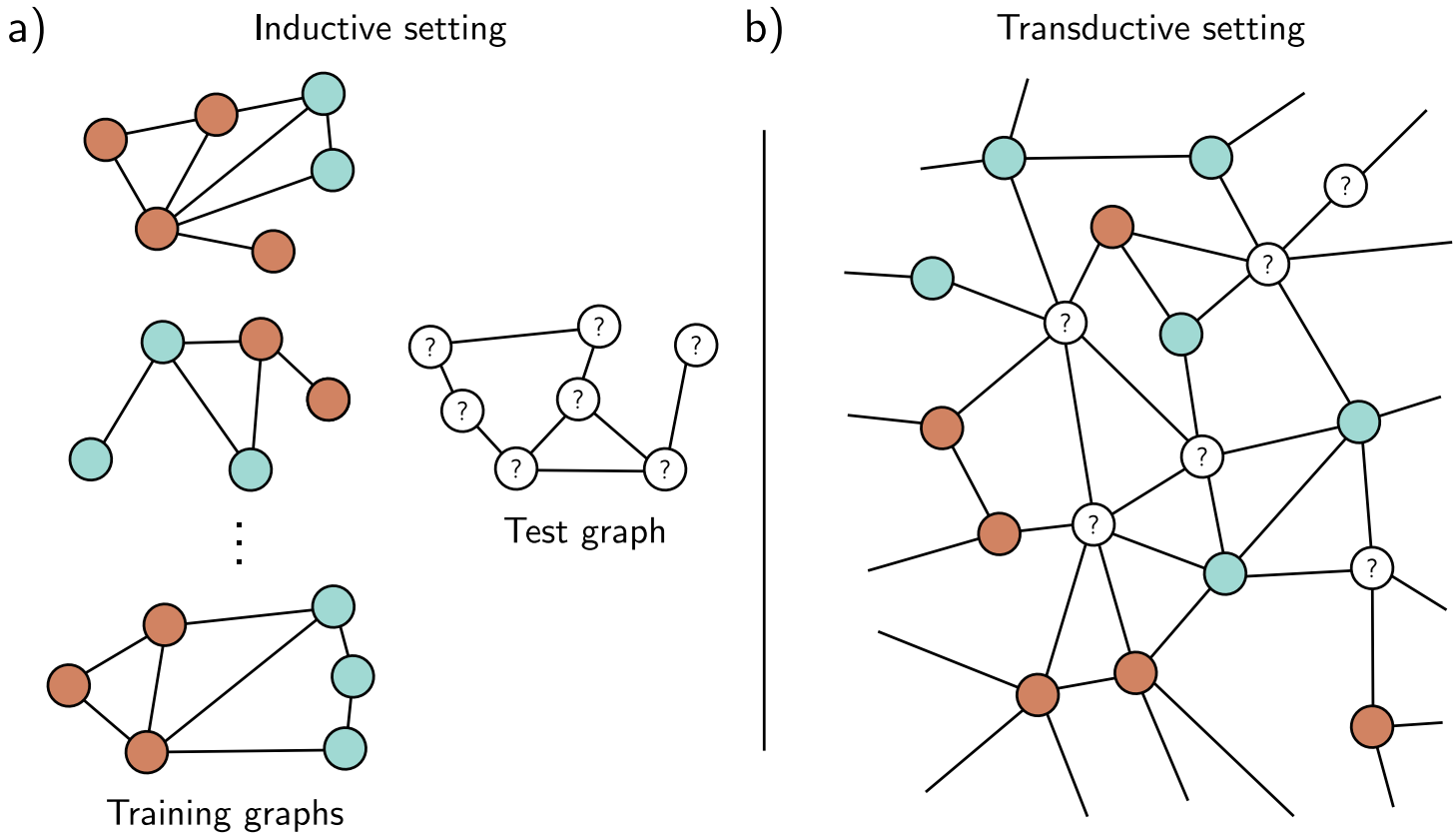
- a) 귀납적 환경에서의 노드 분류 과제이다. 노드 레이블(주황색과 청록색)이 알려진 $I$ 훈련 그래프 세트가 주어진다. 훈련 후에는 test 그래프가 주어지며 각 노드에 레이블을 할당해야 한다.
- b) 귀납적 설정에서의 노드 분류이다. 일부 노드에는 레이블(주황색과 청록색)이 있고 다른 노드는 알 수 없는 큰 그래프가 하나 있다. 알려진 레이블을 정확하게 예측하도록 모델을 훈련한 다음 알 수 없는 노드에서 예측을 검사한다.
| 특징 | Inductive 모델 | Transductive 모델 |
| 정의 | 훈련 세트의 라벨이 지정된 데이터를 사용하여 입력과 출력 간의 관계를 학습하고 이를 새로운 테스트 데이터에 적용 | 라벨이 지정된 데이터와 라벨이 지정되지 않은 데이터를 동시에 고려하여 학습. 규칙을 학습하기보다는 미지의 출력에 라벨을 할당 |
| 장점 | 새로운 데이터에 학습된 규칙을 적용할 수 있음 | 라벨이 지정되지 않은 데이터의 패턴을 활용하여 의사결정에 사용할 수 있음 |
| 단점 | 테스트 데이터가 훈련 데이터와 분리되어 있어야 함 | 새로운 라벨이 지정되지 않은 데이터가 추가될 때마다 모델을 다시 학습해야 함 |
| 적용 예시 | 여러 개의 라벨이 지정된 분자 그래프를 학습하여 새로운 분자 그래프의 독성 여부를 예측 | 큰 단일 그래프(예: 과학 논문의 인용 네트워크)에서 일부 노드에 라벨이 있고, 나머지 노드의 라벨을 예측 |
| 손실 함수 | 입력과 출력 간의 관계를 학습하여 새로운 데이터에 적용 | 모델 출력과 알려진 라벨 간의 불일치를 최소화, 포워드 패스를 통해 미지의 노드에 대한 결과 예측 |
| 그래프 레벨 작업 | O | X |
| 노드 레벨 작업 | O | |
| 엣지 예측 작업 | O | |
7. Example: node classification
수백만 개의 노드에 대하여 일부 레이블이 없는 노드를 분류하는 transductive 모델에 대해서 생각해 보자. 이 네트워크를 훈련하면 두 가지 문제가 발생한다.
- 첫째, 이 크기의 그래프 신경망을 훈련하는 것은 논리적으로 어렵다. 포워드 패스의 모든 네트워크 계층에 노드 임베딩을 저장해야 한다고 생각해 보자. 이렇게 하면 전체 그래프 크기의 몇 배에 달하는 구조를 저장하고 처리해야 하는데, 이는 실용적이지 않을 수 있다.
- 둘째, 그래프가 하나뿐이므로 확률적 경사 하강을 수행하는 방법이 명확하지 않다. 객체가 하나만 있는 경우 어떻게 배치를 구성할 수 있을까?
6.1. Choosing batches
문제점: 큰 그래프의 처리
- 상업용 크기의 그래프에는 수백만 개의 노드가 포함될 수 있으며, 모든 노드 임베딩을 각 네트워크 레이어에 저장하고 처리하는 것은 비현실적이다.
- 단일 그래프만 있을 때, 배치를 어떻게 구성할지 불명확하다. 이는 그래디언트 하강법(Stochastic Gradient Descent, SGD)을 수행하는 데 어려움을 준다.
해결책: 배치 선택
- 무작위로 라벨이 지정된 노드 선택
- 각 학습 단계마다 무작위로 라벨이 지정된 노드의 부분 집합을 선택한다.
- 선택된 각 노드는 이전 레이어에서 이웃 노드들의 영향을 받으며, 이 과정은 반복된다. 이렇게 하면 각 노드가 수용 필드(receptive field)를 갖게 된다.
- 수용 필드 (Receptive Fields)
- 수용 필드는 각 노드가 영향을 받는 그래프의 부분을 의미한다. 이는 합성곱 신경망(CNN)에서의 수용 필드와 유사하다.
- k-홉 이웃(k-hop neighborhood)이라 불리는 이 수용 필드는 선택된 노드와 k-홉 이내의 이웃 노드들로 구성된다.
- 그래프 확장 문제:
- 그래프가 밀집되어 있는 경우, 수용 필드가 모든 입력 노드를 포함할 수 있다. 이는 그래프 크기를 줄이는 데 도움이 되지 않는다. 이를 그래프 확장 문제(graph expansion problem)라고 한다.
- 해결 방법:
- Neighborhood Sampling: 배치의 노드를 선택한 후, 각 노드의 이웃을 샘플링하여 그래프의 크기를 제한한다. 이는 드롭아웃(dropout)과 유사하며 정규화 효과를 준다.
- 예: 배치 노드에서 무작위로 이웃 노드를 샘플링하고, 다시 그 이웃의 이웃을 샘플링하여 점진적으로 그래프를 축소한다.
- Graph Partitioning: 원래 그래프를 서로 연결되지 않은 작은 하위 그래프로 분할한다. 이 작은 그래프들은 배치로 처리되며, 각 하위 그래프는 독립적으로 학습된다.
- 예: 그래프를 분할하여 최대한 내부 링크를 유지하는 알고리즘을 사용하고, 분할된 하위 그래프를 배치로 처리한다. 이때, 하위 그래프의 쌍을 배치로 활용하면 내부 링크를 보존할 수 있다.
- Neighborhood Sampling: 배치의 노드를 선택한 후, 각 노드의 이웃을 샘플링하여 그래프의 크기를 제한한다. 이는 드롭아웃(dropout)과 유사하며 정규화 효과를 준다.
8. Layers for graph convolutional networks
이전 예제에서는 단순히 노드 임베딩 행렬 $\mathbf{H}$에 인접 행렬 $\mathbf{A}$와 항등 행렬 $\mathbf{I}$를 더한 행렬을 곱하여 이웃 노드의 정보를 집계했다. 이제는 GNN의 성능을 향상시키기 위해 (i) 현재 노드 임베딩과 집계된 이웃 노드 임베딩을 결합하는 측면과 (ii) 이웃 노드 임베딩을 집계하는 측면에 있어서 여러가지 다양한 방법이 존재하지만 이는 생략하도록 하겠다.
9. Edge graphs
9.1. 기본 아이디어
기존의 GNN은 주로 노드 임베딩을 처리하지만, 많은 그래프 문제에서는 엣지(노드 간의 연결)에 대한 정보도 중요하다. 엣지 그래프는 원래 그래프의 엣지를 노드로 변환하여, 엣지에 대한 임베딩을 처리할 수 있도록 한다.
9.2. 엣지 그래프 생성
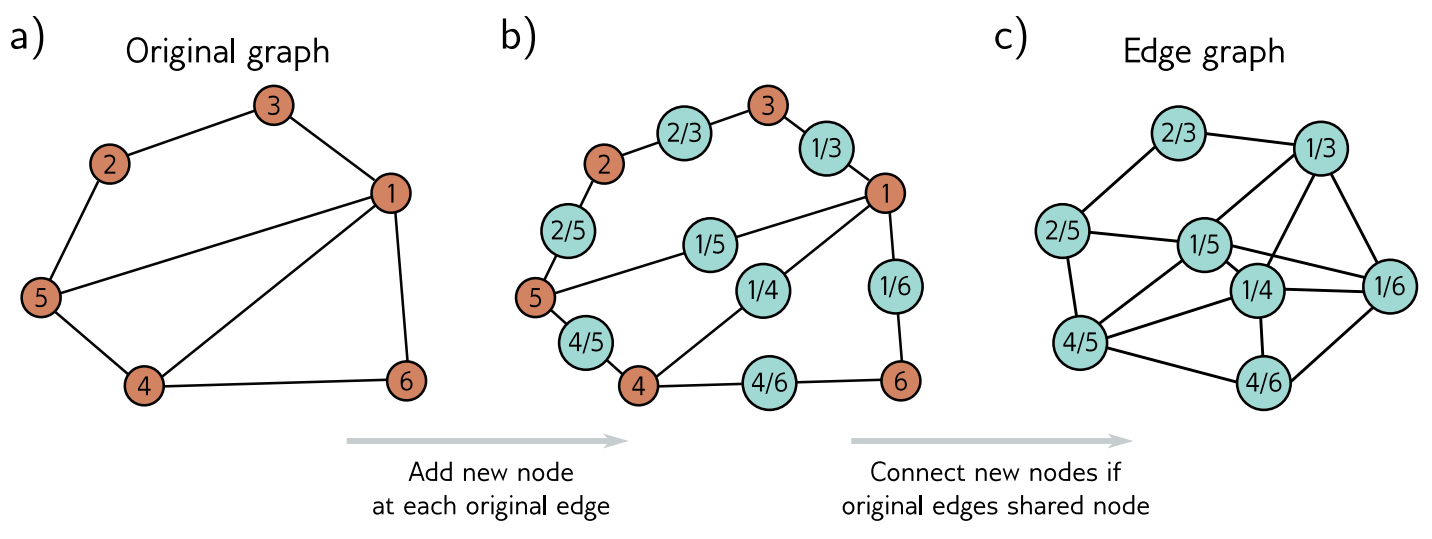
원본 그래프의 엣지 변환
원본 그래프의 각 엣지는 엣지 그래프에서 하나의 노드로 변환된다. 원본 그래프의 두 엣지가 공통 노드를 가질 때, 엣지 그래프에서는 이 두 엣지가 서로 연결된다.
예를 들어, 원래 그래프에서 노드 $u$와 노드 $v$를 연결하는 엣지가 있을 때, 엣지 그래프에서는 이 엣지가 하나의 노드가 된다. 만약 원래 그래프에서 노드 $v$와 노드 $w$를 연결하는 또 다른 엣지가 있다면, 엣지 그래프에서는 이 두 엣지(노드)가 연결된다.
엣지 그래프의 활용
엣지 그래프를 생성하면, 원래 그래프의 엣지를 노드로 처리할 수 있다. 이를 통해 엣지 임베딩을 업데이트하거나, 엣지의 특성을 학습할 수 있다.
엣지 그래프에서의 처리
엣지 그래프를 사용하면 다음과 같은 네 가지 업데이트를 수행할 수 있다:
- 노드가 노드를 업데이트: 기존 GNN 방식으로 노드 임베딩을 업데이트한다.
- 노드가 엣지를 업데이트: 노드 임베딩을 사용하여 엣지 임베딩을 업데이트한다.
- 엣지가 노드를 업데이트: 엣지 임베딩을 사용하여 노드 임베딩을 업데이트한다.
- 엣지가 엣지를 업데이트: 엣지 그래프를 사용하여 엣지 임베딩을 업데이트한다.
이 과정에서 노드와 엣지 임베딩 간의 상호작용을 통해 더 풍부한 정보를 학습할 수 있다.
스터디 핵심
- 그래프에서 노드와 엣지를 사용해 데이터의 특징이 주어졌으므로, 이를 최대한 활용할 수 있는 모델로서 GNN이 고안되었다.
- 그래프는 노드와 엣지의 개수가 각각 다르므로, 일관적인 연산을 정의하기 위해 집계(어그리게이션)한 후, 웨이트를 곱하는 방식을 사용했다.
- 그러나 이후 어텐션 메커니즘이 개발되면서 집계 연산을 대체하게 되었다. 어텐션을 사용하면 각 노드가 중요하다고 판단하는 이웃 노드의 정보에 가중치를 부여할 수 있다. 이는 마치 그래프에서의 관계를 학습하는 것과 유사하다.
- 또한 인접 행렬을 마치 마스크처럼 사용하여 필요한 노드들 간의 상호작용을 효과적으로 학습하도록 하는 아이디어가 고안되었다.
- 결과적으로, 전통적인 어그리게이션 후 웨이트를 곱하는 방식은 거의 사용되지 않게 되었고, 어텐션 메커니즘이 이를 대신하여 사용되고 있다.
'인공지능 > Deep Learning' 카테고리의 다른 글
| Feature Pyramid Networks for Object Detection (2) | 2024.02.09 |
|---|---|
| CIDEr-D와 METEOR (0) | 2023.10.05 |
| MLP 모델의 Weight Initialization에 대한 이해 (0) | 2022.07.05 |
| Output units - Sigmoid Unit & Softmax Unit (0) | 2022.06.22 |





